My two previous posts on p-zombies and homunculus actors have been attempts to lay a little philosophical groundwork, imagining some possibilities in which you appear to go on into the future even though you are annihilated. The point of these is to try to provide a refined form of an argument I visited some years ago called the Mephistopheles wager. The idea behind that wager, for those of you who have never heard of it or who have quite forgivably forgotten, this Mephistopheles wager was a bet taken at some probability p such if you won the bet with probability (1-p) you would get something you wanted, needed, sought, or so forth and otherwise with probability p you would be instantly and painlessly annihilated. Since even your instant and painless annihilation would leave bereaved loved-ones behind, I conjured up some exotic possibilities called the p-zombie and the homunculus actor, which between them, make for a better mechanism of self-annihilation than just being dead, because your loved ones need never know that you lost the wager. From their perspectives, you’ll be going on as before. Call p-zombies and homonculus actors, therefore, a BATDAPE, a Best Alternative to Death as Personal Extinction. We can therefore refine the Mephistopheles wager to understand that if you win, you get what you wanted, and if you lose, BATDAPE for you.
Now we might well imagine a cumulative Mephistopheles wager, that is to say perhaps, many small wagers that add up to a larger one: for example, you’d take a Mephistopheles wager with a probability of 0.1 if the prize is a really awesome romantic partner (in place, perhaps, of a lifetime of loneliness), a probability of 0.2 of having a career that is at once well-remunerated, meaningful, and enjoyable (as opposed to a lifetime of crappy work). All these wagers could be added up to your Cumulative Lifetime Mephistopheles Wager.
Now my intuition, way back when, was that if you would take a Cumulative Lifetime Mephistopheles wager of 0.5 or greater, then in some important sense your life is a misfortune. There are various informal ways to try to justify this intuition — think, for example, how desperate and miserable you would have to be to play a single round of Russian roulette, with say, a prize of ten million dollars offered if you survive — and that’s a just a wager with probability of 0.17 (assuming a fair six-chambered revolver). But here is a way in which I think that the intuition might be justified more formally.
Everyone’s life is a combination of satisfactions and frustrations. Satisfactions are things that make you happy (good food, time with friends, good sex, etc.) or which make your life seem to mean something to you (you teach inner-city children to read, visit and provide company for lonely old people, make scientific discoveries, adopt puppies and kittens otherwise fated for destruction). It take it every life has at least some satisfactions, and some have many. The satisfactions of your life have a magnitude, which is to say some measure of their overall size. The magnitude is probably best characterized as an ordinal measure of sorts: while only the most aggressive utilitarians would be willing to attach a number to each individual satisfaction and then treat the magnitude as an arithmetic sum of those, most of the rest of us would still be able to say that adding a certain condition to our lives either makes our satisfactions greater or less, and to compare adding one or the other and seeing whether their addition to our life’s satisfactions be greater or less for one or the other, or equal for both.
Life is also characterized by frustrations. These have both a positive an a negative character. Life’s positive frustrations are bad things we wish we could remove but can’t. They might be personal forms of unhappiness like persistent physical pain or debility or loneliness, Or there are negative frustrations, things we desire or need but can’t achieve: real success in a career that matters to us, or a happy relationship with someone. There might even be global meaning frustrations to our lives: we really want to get rid of war or poverty or political oppression but just can’t and feel helpless and angry as a result of these. Like satisfactions our life’s frustrations have a magnitude, again probably of an ordinal character: add this frustration to life and our lives are worse, add another one and our lives are worse still even if the first frustration is not added, and so on.
Magnitudes of satisfactions and frustrations matter. Imagine a hypothetical life that had in it only satisfactions. Would we say that life is a misfortune? I would concede that it is not. Indeed, I would concede that we could add some minor frustrations to that life and it would still not be a misfortune. But surely we cannot add on frustrations to that life without end without at some point deeming that life to be a misfortune. The contrary position is subject to a straightforward reductio: if you believe that no amount of frustrations make a life a misfortune, then you’re committed to a view that life could have infinite frustrations — infinite suffering — and that’s absurd.
At what point might someone say that a life is a misfortune? It is clearly at some point between null and infinite magnitudes of frustration. While I suppose that there might be other possible answers, the only one that seems intuitively plausible to me would be the point at which the magnitude of one’s frustrations becomes greater than than of one’s satisfactions.
If the magnitude of your frustrations exceeds that of your satisfactions, then your life is a misfortune. And that, I think, is about intuitive rock-bottom for me.
Well and good, but that just seems to bring up the question of how one compares magnitudes of things like satisfactions and frustrations. The answer to that question would seem to be “what bet would you take?”
If it seems absurd to talk about what bets one would take in a context where what is at stake is your future existence, reflect: in a small way we are taking bets that resemble the Mephistopheles wager all the time. Have you ever crossed a busy street to buy a cup of coffee and a newspaper? Well, then you’ve taken a bet that you won’t be run down by a car. Maybe in most circumstances that’s a pretty good bet, but it’s still a bet. In taking that action you are accepting a (very small, one hopes) probability of having no future in order to turn a frustration (lack of coffee and news) into a satisfaction. You might not want to think about it as a bet, but a bet it is, and in some situations the risk will become sufficiently salient that the bet-like character of the action will become apparent. You might cross a busy street to get a cup of coffee and a newspaper, but you would be unlikely to want to cross an active minefield for the same. Then again, if what’s on the other side of that minefield is sufficiently important to you, you might very well cross it: if what’s on the other side isn’t just coffee and a newspaper but your badly-wounded, will-die-if-she-doesn’t-receive-medical-attention child, then you might very well plunge forward and take the risk. The risks we take are the mechanism for revealing what it is that matters to us.
Now there’s a special sort of bet that becomes rational when the magnitude of what we win matches the magnitude of what we stand to lose, the so-called double-or-nothing bet, that is, the bet that we might take when the odds of losing are 0.5. Consider a very simple kind of person, Homo economicus, who is only interested in maximizing how much money he has. If you offer Homo economicus an opportunity to spend his $4 in wealth that wins lottery ticket that wins with a probability of 0.5, how much would the jackpot have to be to induce him to buy? Answer: at least $8.01, because the expected value of the ticket for Homo economicus can be calculated simply as p(win)*jackpot, so 0.5*$8.01 = $4.005 > $4. For that value, Homo economicus would give up the satisfaction that matters to him (possession of $2) to get rid of the frustration he has (of $2.01 that isn’t his but might be).
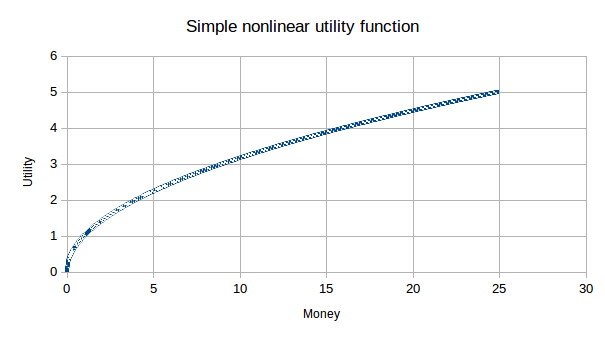
Few people would be so simple as Homo economicus. Consider a cousin of Homo economicus, Homo prudens, who doesn’t value only money, but cares about what money can get him — about money’s utility, in other words. The more money Homo prudens has, the less valuable it is to him, though more is always better. Homo prudens might have a utility function like this:
Note, however, that there is still a double-or-nothing bet that Homo prudens might take if his wealth is $4, which is to say one which pays off $16 if it wins. The magnitude of the utility of $8 isn’t enough, but whatever frustrations Homo prudens could make go away with $16.01 in wealth would make it worth it to him to take the bet. That would thus seem to be the point at which the magnitude of his frustrations equals that of his satisfactions.
That’s enough for one post on the matter. On a post shortly to come, I’ll try to address the question of whether it’s just crazy to use examples like this to evaluate actual human lives.