My two previous posts on p-zombies and homunculus actors have been attempts to lay a little philosophical groundwork, imagining some possibilities in which you appear to go on into the future even though you are annihilated. The point of these is to try to provide a refined form of an argument I visited some years ago called the Mephistopheles wager. The idea behind that wager, for those of you who have never heard of it or who have quite forgivably forgotten, this Mephistopheles wager was a bet taken at some probability p such if you won the bet with probability (1-p) you would get something you wanted, needed, sought, or so forth and otherwise with probability p you would be instantly and painlessly annihilated. Since even your instant and painless annihilation would leave bereaved loved-ones behind, I conjured up some exotic possibilities called the p-zombie and the homunculus actor, which between them, make for a better mechanism of self-annihilation than just being dead, because your loved ones need never know that you lost the wager. From their perspectives, you’ll be going on as before. Call p-zombies and homonculus actors, therefore, a BATDAPE, a Best Alternative to Death as Personal Extinction. We can therefore refine the Mephistopheles wager to understand that if you win, you get what you wanted, and if you lose, BATDAPE for you.

Now we might well imagine a cumulative Mephistopheles wager, that is to say perhaps, many small wagers that add up to a larger one: for example, you’d take a Mephistopheles wager with a probability of 0.1 if the prize is a really awesome romantic partner (in place, perhaps, of a lifetime of loneliness), a probability of 0.2 of having a career that is at once well-remunerated, meaningful, and enjoyable (as opposed to a lifetime of crappy work). All these wagers could be added up to your Cumulative Lifetime Mephistopheles Wager.

Now my intuition, way back when, was that if you would take a Cumulative Lifetime Mephistopheles wager of 0.5 or greater, then in some important sense your life is a misfortune. There are various informal ways to try to justify this intuition — think, for example, how desperate and miserable you would have to be to play a single round of Russian roulette, with say, a prize of ten million dollars offered if you survive — and that’s a just a wager with probability of 0.17 (assuming a fair six-chambered revolver). But here is a way in which I think that the intuition might be justified more formally.

Everyone’s life is a combination of satisfactions and frustrations. Satisfactions are things that make you happy (good food, time with friends, good sex, etc.) or which make your life seem to mean something to you (you teach inner-city children to read, visit and provide company for lonely old people, make scientific discoveries, adopt puppies and kittens otherwise fated for destruction). It take it every life has at least some satisfactions, and some have many. The satisfactions of your life have a magnitude, which is to say some measure of their overall size. The magnitude is probably best characterized as an ordinal measure of sorts: while only the most aggressive utilitarians would be willing to attach a number to each individual satisfaction and then treat the magnitude as an arithmetic sum of those, most of the rest of us would still be able to say that adding a certain condition to our lives either makes our satisfactions greater or less, and to compare adding one or the other and seeing whether their addition to our life’s satisfactions be greater or less for one or the other, or equal for both.

Life is also characterized by frustrations. These have both a positive an a negative character. Life’s positive frustrations are bad things we wish we could remove but can’t. They might be personal forms of unhappiness like persistent physical pain or debility or loneliness, Or there are negative frustrations, things we desire or need but can’t achieve: real success in a career that matters to us, or a happy relationship with someone. There might even be global meaning frustrations to our lives: we really want to get rid of war or poverty or political oppression but just can’t and feel helpless and angry as a result of these. Like satisfactions our life’s frustrations have a magnitude, again probably of an ordinal character: add this frustration to life and our lives are worse, add another one and our lives are worse still even if the first frustration is not added, and so on.

Magnitudes of satisfactions and frustrations matter. Imagine a hypothetical life that had in it only satisfactions. Would we say that life is a misfortune? I would concede that it is not. Indeed, I would concede that we could add some minor frustrations to that life and it would still not be a misfortune. But surely we cannot add on frustrations to that life without end without at some point deeming that life to be a misfortune. The contrary position is subject to a straightforward reductio: if you believe that no amount of frustrations make a life a misfortune, then you’re committed to a view that life could have infinite frustrations — infinite suffering — and that’s absurd.

At what point might someone say that a life is a misfortune? It is clearly at some point between null and infinite magnitudes of frustration. While I suppose that there might be other possible answers, the only one that seems intuitively plausible to me would be the point at which the magnitude of one’s frustrations becomes greater than than of one’s satisfactions.

If the magnitude of your frustrations exceeds that of your satisfactions, then your life is a misfortune. And that, I think, is about intuitive rock-bottom for me.

Well and good, but that just seems to bring up the question of how one compares magnitudes of things like satisfactions and frustrations. The answer to that question would seem to be “what bet would you take?”

If it seems absurd to talk about what bets one would take in a context where what is at stake is your future existence, reflect: in a small way we are taking bets that resemble the Mephistopheles wager all the time. Have you ever crossed a busy street to buy a cup of coffee and a newspaper? Well, then you’ve taken a bet that you won’t be run down by a car. Maybe in most circumstances that’s a pretty good bet, but it’s still a bet. In taking that action you are accepting a (very small, one hopes) probability of having no future in order to turn a frustration (lack of coffee and news) into a satisfaction. You might not want to think about it as a bet, but a bet it is, and in some situations the risk will become sufficiently salient that the bet-like character of the action will become apparent. You might cross a busy street to get a cup of coffee and a newspaper, but you would be unlikely to want to cross an active minefield for the same. Then again, if what’s on the other side of that minefield is sufficiently important to you, you might very well cross it: if what’s on the other side isn’t just coffee and a newspaper but your badly-wounded, will-die-if-she-doesn’t-receive-medical-attention child, then you might very well plunge forward and take the risk. The risks we take are the mechanism for revealing what it is that matters to us.

Now there’s a special sort of bet that becomes rational when the magnitude of what we win matches the magnitude of what we stand to lose, the so-called double-or-nothing bet, that is, the bet that we might take when the odds of losing are 0.5. Consider a very simple kind of person, Homo economicus, who is only interested in maximizing how much money he has. If you offer Homo economicus an opportunity to spend his $4 in wealth that wins lottery ticket that wins with a probability of 0.5, how much would the jackpot have to be to induce him to buy? Answer: at least $8.01, because the expected value of the ticket for Homo economicus can be calculated simply as p(win)*jackpot, so 0.5*$8.01 = $4.005 > $4. For that value, Homo economicus would give up the satisfaction that matters to him (possession of $2) to get rid of the frustration he has (of $2.01 that isn’t his but might be).

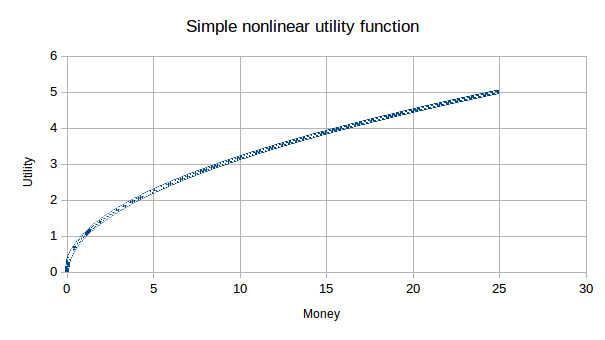
Few people would be so simple as Homo economicus. Consider a cousin of Homo economicus, Homo prudens, who doesn’t value only money, but cares about what money can get him — about money’s utility, in other words. The more money Homo prudens has, the less valuable it is to him, though more is always better. Homo prudens might have a utility function like this:

Note, however, that there is still a double-or-nothing bet that Homo prudens might take if his wealth is $4, which is to say one which pays off $16 if it wins. The magnitude of the utility of $8 isn’t enough, but whatever frustrations Homo prudens could make go away with $16.01 in wealth would make it worth it to him to take the bet. That would thus seem to be the point at which the magnitude of his frustrations equals that of his satisfactions.

That’s enough for one post on the matter. On a post shortly to come, I’ll try to address the question of whether it’s just crazy to use examples like this to evaluate actual human lives.

And my poor fool is hanged. No, no, no life?
Why should a dog, a horse, a rat have life,
And thou no breath at all? Thou ’lt come no more,
Never, never, never, never, never.—
Pray you undo this button. Thank you, sir.
Do you see this? Look on her, look, her lips,
Look there, look there!

—King Lear, V,iii, 369-75

In his fictional world, Lear no doubt suffers terribly from the death of his daughter Cordelia, but what we really see on the stage is not an actual king but an actor. The actor is himself a conscious human being (presumably), but even if the actor is using the Method we needn’t really believe that the actor is suffering from terrible bereavement.

In my previous post I suggested as a thought experiment for eliciting our values about existence and non-existence we consider the possibility of becoming a p-zombie rather than committing suicide. In the p-zombie thought experiment a non-conscious simulactrum of ourselves would go forward into the future leaving all the people in our lives none-the-wiser about our status. Becoming a p-zombie would thus have the advantage of allowing us to terminate our own suffering without causing bereavement and misery among our surviving friends and family. A commenter objected that he found the idea of a p-zombie so deeply implausible that the thought the entire thought experiment made no sense. I’m not sure I agree with that, but in the interest of moving forward I’ll offer here an alternative thought experiment.

Suppose that there is a being that we could call a Consummate Homunculus Actor, for short, “Cohom.” Knows you in excruciating detail, has access to all your memories, knows all your likes and dislikes, appetites and aversions, phobias and kinks, and can there act the part of you with such fantastic fidelity that external observers can’t tell the difference between you and a kind of high-fidelity puppet whose strings are pulled by Cohom. Cohom is not a zombie. Cohom is conscious, but conscious in the sense that our actor playing Lear is conscious. He’s very much aware of what he’s doing when he’s playing Lear, but he isn’t actually suffering in anything like the sense that Lear is suffering.

Now suppose you had this alternative. Cohom could crawl inside your head, wipe your own consciousness, pick up the reins of your behavior, and act out the complicated part that is you living out your life. Because Cohom knows everything that’s relevant about you, the people around you will never know that it’s Cohom discoursing with or reacting to them, rather than “you.” Cohom will see through “your” eyes and feel with “your” hands, but will not feel pain or love or anything like that directly. Rather, “your” burning your hand on a stove will be an event in a script to which Cohom must respond with an appropriate yowl of pain. The same for “your” falling in love. For Cohom it’s a part to be acted. The balance of your life might be something like The Truman Show except inverted. Instead of “you” being “real” and everyone around you being an actor hired to play a part, “you” will be an actor and everyone else around you will be “real.” The “real” you will have long since departed into the blessed calm of eternal unconsciousness. Cohom, meanwhile, will stay on the job until “your” death, at which point he collects a handsome check from whatever mad or demonic employer engaged his services in playing the part of you, and possibly an acting award as well.

Cohom or p-zombie, either way you get an out.

There’s a sort of creature invented by philosophers called philosopher’s zombie or a p-zombie for short. The p-zombie, unlike say the movies featured in movies by George Romero (may he rest in peace), are not shambling, stupid, re-animated corpses. Rather, they’re people just like you or me except in one respect: they are completely unconscious. They have no inner life, no feelings, no memories, no imaginations, none of that. But in spite of not having an inner life, they are behaviorally identical to people who do have inner lives. Poke one with a pin and it will say “ouch” and act indignant with you, as if it were really feeling pain. Ask a p-zombie about a sad incident in its childhood and it may be able to do so, perhaps with tears in its eyes. But it is not “remembering” its childhood anymore than a record player is “remembering” the contents of a disk it is playing, and it is not sad any more than a classically-trained actor playing Lear is actually mourning Cordelia.

You can’t tell a p-zombie from a “real” person by observing what it does, because what it does is the same thing a as “real” person. More unsettling than that, you can’t somehow peer inside someone and tell whether or not they are a “real” person or a p-zombie. Look inside a “real” person’s brain, and all you will see are a bunch of cells squirting electrochemical signals at one another. A p-zombie’s brain is just the same way. In neither case can you observe a “mind,” see a “person,” or observe “feelings.” To be sure, you might come to confident that certain brain-states correlate reliably with states of mind. You might, for example, come to believe based on evidence from a long series of tests that a certain neuronal firing pattern is someone thinking of a white bear. But this again is only correlations of observed behaviors: when the state is observed, the subject reports thinking of a white bear. The problem is that p-zombies just as readily as “real” people can report thinking of a white bear. It’s just that the p-zombie is not really thinking of anything at all, while the “real” person is. In neither case do you actually see something inside the head that looks like a white bear, or directly observe the White Bear State of Mind.

Most philosophers think that p-zombies are physically impossible and can’t exist in our world, and at least some think that they are metaphysically impossible, that is, that they can’t exist in any possible world. One has to admit that the p-zombie is a pretty unsettling concept. Anyone you know could (in theory, anyway) be not a person, but a p-zombie. Your boss. Your parents. Your spouse. Your adorable toddler daughter who says “I wuv you” as she drifts off to sleep in your arms might not love you at all, but just be a piece of machinery carrying out its programming, unfeeling as any rock.

The concept of the p-zombie makes an interesting thought experiment possible. Suppose there were a drug that could turn you, permanently, instantly, and irrevocably into a p-zombie. Upon taking a does of the drug your consciousness would be instantly annihilated and gone for good. But no one would ever actually be able to tell that you had taken the drug. Future history will be exactly the same as if you had not done so, because the p-zombie that was you will behave exactly as you would have behaved. It will continue to get up in the morning, catch the train to work, stand around the watercooler with colleagues griping about the boss, come home in the evenings, help its children with their homework, have increasingly dutiful and diminishingly frequent sex with your spouse, age, retire, move to the Sunbelt, collect various government benefits, and die, just like you would have. Through all of this, “you” will be gone, together with all the joys and sufferings the balance of your life might contain. The p-zombie will act happy or sad or angry, happy at your daughter’s wedding or angry during its periodic quarrels with your spouse. But it just as much as you will live in the blessed calm of complete consciousness.

Thus p-zombification might be thought of not so much as a kind as an alternative to suicide, and leads me to wonder whether if it were somehow available, it wouldn’t cut off a slice both of suicides and non-suicides. I should think it would do both, and my reason for thinking so is at least in part autobiographical. At the closest I ever personally came to suicide, around the age of thirty or so, the thought that stayed my hand more than any other was that of the suffering that my killing myself would inflict on people I loved, most particularly on my parents (ironic for an antinatalist to feel that way perhaps, but emotional life is messy). I can’t really guarantee that things would have been the same had there been a way out of suffering that they and no one else need ever have known about.

A life is a stone dropped into a pond and its meaning the ripples heading out therefrom.

Heave a brick into the Mississippi at Minneapolis. Have a friend in New Orleans try to distinguish its ripples from everything else in the river. Her report back to you should tell you much about a human life inside human history.

In his most recent book, David Benatar notes that we pessimists actually do pretty well in terms of our behavior. (For “one” in the passage below, we can read “we.”)

One does not enter into people’s houses of worship to tell them they are wrong, or knock on people’s doors offering to share the “bad news” with them. One does not stop pregnant women on the street and excoriate them and their partners for creating new life.^*

Well put, Professor Benatar! I might note that other things we do not do include firebombing maternity wards or gunning down fertility doctors in the lobbies of their churches.

No, we leave all that sort of thing (mutatis mutandis, naturally) to those lovely “pro-life” people.

^*David Benatar, The Human Predicament: A Candid Guide to Life’s Biggest Questions. (New York and Oxford: Oxford University Press, 2017), p. 11. Back to main text.

I probably ought not write about this, because I see it bringing only trouble. But I can be compulsive about the truth as I see it, so…

Young adulthood was pretty good to me. I had an awesome girlfriend and I was beginning to climb the rungs, successfully and almost easily, toward a career that I would have really enjoyed, had things panned out the way I thought they would have. Things started turning south, I would say, at about the age of 24½. For about six years after that, life felt like one heartbreaking disappointment after another.

I am now past 50 years in age, and the following grim reflection occurs to me. Although I am nothing like suicidal now, I do think that if, by some hideous anti-miracle of cognition I could have had in foresight at the age of 24½ the quarter-century I now have in hindsight, and had efficient means been available — such as a fistful of Nembutal or a reliable firearm — I very well might have killed myself. At least, the resolution to do so I regard as retrospectively rational. That I did not do so is a tribute not to wisdom but to ignorance and I suppose also to hope — here the irrational conviction during my darkest days that things would look up someday, that at the end of all the misery there would be a life so much better that I would be glad to have persevered through wretchedness. That isn’t so. While in fact things did get somewhat better, I do not now regard them as so much better that it was worth it to have lived through the darkest days. And I certainly no longer expect that any good thing lies in my future that will change this judgment. No lottery wins or Nobel Prizes lurk over my horizon, and don’t let me get started on my pessimism about relationships.

Life is served by ignorance and irrationality. That doesn’t say much good about life.

Update on July 20, 2017. I’ve added a link above about my pessimism about relationships. And if you like that sort of thing, here’s another.

The philosopher Eric Schwitzgebel has written a post recently (H/t to Brian Leiter) responding to recent books written by Owen Flanagan (The Geography of Morals, 2016) and Paul Bloom (Against Empathy, also 2016). To oversimply grossly, these two writers think we would be better off getting rid of certain kinds of emotion, in Flanagan’s case anger and in Bloom’s case empathy. Flanagan thinks we would be better off striving to become like Buddhist or Stoic sages, and Bloom thinks we could achieve a good society better using cool, rational compassion in place of empathy in making social decisions.

Perhaps unsurprisingly, Professor Schwitzgebel doesn’t like these proposals very much. He advances (though admits he doesn’t at the moment have an argument for defending) a view that the world would in an important sense be poorer without these emotions even if getting rid of them might in some sense make the world better. He thinks that there is an intrinsic value to having a “rich” world, and articulates his understanding thusly:

I want to push back against the idea that we should narrow the emotional range of our lives by rejecting empathy and anger. My thought is this: Having a rich emotional range is intrinsically valuable.

One way of thinking about intrinsic value is to consider what you would wish for, if you knew that there was a planet on the far side of the galaxy, beyond any hope of contact with us. (I discuss this thought experiment here and here.) Would you hope that it’s a sterile rock? A planet with microbial life but not multi-cellular organisms? A planet with the equivalent of deer and cows but no creatures of human-like intelligence? Human-like intelligences, but all lying comatose, plugged into simple happiness stimulators?

Here’s what I’d hope for: a rich, complex, multi-layered society of loves and hates, victories and losses, art and philosophy, history, athletics, science, music, literature, feats of engineering, great achievements and great failures. When I think about a flourishing world, I want all of that. And negative emotions, destructive emotions, useless bad stuff, those are part of it. If I imagine a society with rational compassion, but no empathy, no anger — a serene world populated exclusively by Buddhist and Stoic sages — I have imagined a lesser world. I have imagined a step away from all the wonderful complexity and richness of life.

Most of Professor Schwitzgebel’s commenters seem to agree that the “wonderful complexity and richness of life” seems to trump any advantages to getting rid of things like anger.

My response to Professor Schwitzgebel’s though experiment is the good antinatalist one: “sterile rock, please.” I do find it entertaining how the way the experiment was set up allows me to echo Schopenhauer.

Note on the texts

I’m not about to offer a global defense of my view any more than Professor Schwitzgebel is of his, but I will offer first this observation: the “rich, wonderful world” that Professor Schwitzgebel imagines is surely one containing a lot of suffering. I don’t think Professor Schwitzgebel would deny this claim and indeed language like “…negative emotions, destructive emotions, useless bad stuff, those are part of it” seems to admit it, but to expand a bit on the point. The existence of anger — at least, any sort of anger that is somehow rationally motivated — seems to require the existence of suffering, something for people to be angry at, and seem also likely to be the cause of suffering as people act on that anger or, alternatively, bottle it up and stew. An empathy, if it’s to have much of a positive point, needs suffering to empathize with.

Having made that observation, I’m inclined to offer an error theory for why it is that people can believe that it’s so great to have a “rich, wonderful world,” and it’s that when people are allowed to contemplate cruelty and suffering as spectators, rather than as people who have to undergo the suffering, it turns out that they rather enjoy the spectacle. Our literature abounds in atrocity: from the Iliad to the latest action-movie productions of Hollywood, violence and death draw eager audiences. Those pages of history are most avidly read that are written in blood, whereupon are chronicled stories of war, massacre, and persecution. Our sporting events, from gladiatorial combats to American football, are given their seasoning by the prospect of injury and pain. And, without going too deeply into the politics of the present day, I must observe that much current political behavior is at best hard to explain if we do not take into account how the winners in political struggles savor, if only through their television screens, the sufferings inflicted on the losers. Old Nietzsche was right: spectatorial cruelty is woven deep into our natures. Small wonder people like Professor Schwitzgebel and his commenters want the “rich” world. It gives them something fun to look at, or at least contemplate within the confines of their imaginations. Honestly, it is all enough to make one sympathetic to that dark kind of antinatalism.

Let me say that I do not for a minute that I do not think for a minute that I am a better person than Professor Schwitzgebel or his commenters. I have just as much spectatorial cruelty in my nature as they, perhaps more, as a quick glance at at least one of my other blogs will quickly reveal. If I differ from them, it is only in my unwillingness to think well of myself.

—

Note on Schopenhauer’s text:

The German text is taken from this online version of his Parerga und Paralipomena under the heading Nachträge zur Lehre vom Leiden der Welt (§156). It represents my own transcription from the rather painful-to-read original Fraktur text. I have tried to follow the punctuation of the original. In one instance I have taken the liberty of updating Schopenhauer’s spelling (from “Noth” to “Not”). The words “…a disappointment, nay a cheat” are in English in Schopenhauer’s original text. The English text is from a translation by Thomas Bailey Saunders, published as “On the Sufferings of the World,” published at Wikisource. Both texts were accessed on March 15, 2017.

Return to main text.

From a recent article in the Health section of The New York Times: “Pregnancy Changes the Brain in Ways That May Help Mothering.”

Pregnancy changes a woman’s brain, altering the size and structure of areas involved in perceiving the feelings and perspectives of others, according to a first-of-its-kind study published Monday.

Most of these changes remained two years after giving birth, at least into the babies’ toddler years. And the more pronounced the brain changes, the higher mothers scored on a measure of emotional attachment to their babies.

[…]

In the study, researchers scanned the brains of women who had never conceived before, and again after they gave birth for the first time. The results were remarkable: loss of gray matter in several brain areas involved in a process called social cognition or “theory of mind,” the ability to register and consider how other people perceive things.

[…]

A…possibility is that the loss is “part of the brain’s program for dealing with the future,” [Paul Thompson, a neuroscientist at the University of Southern California] said. Hormone surges in pregnancy might cause “pruning or cellular adaptation that is helpful,” he said, streamlining certain brain areas to be more efficient at mothering skills “from nurturing to extra vigilance to teaching.”

Another story, from the Guardian, “Pregnancy causes long-term changes to brain structure, says study”, adds some detail.

While the researchers say the lack of similar brain changes among new fathers suggests the adjustments are down to biological processes, such as fluctuations in hormones,[Cambridge University neuroimaging expert Dr. Kirstie] Whitaker points out that environmental influences could be at play. But she agrees with the authors’ suggestion that decrease in grey matter volume could be linked to evolutionary pressures.

“Being a new mum is hard and you have to adjust an awful lot,” said Whitaker. “Your brain is going to be able to respond to that change and it is going to make it so that you can take care of this newborn bundle of joy.”

Now to be sure, it is only one study with a relatively small number of subjects, and we should generally be skeptical of reports in popular media on new science. (I have included the Times‘s link to the underlying Nature paper so readers so inclined may follow that in detail). But let’s grant for the sake of argument that the researchers are onto something and Nature really is hacking pregnant women’s brains in the service of making them better mothers. That possibility prompts (for me, anyway) the following reflection.

At this time there circulate among a certain subset of men who identify as “pick-up artists” or “men’s rights activists” putative techniques for hacking women’s brains in order to increase their sexual availability to the would-be hackers. Decent people generally see these attempts at mind-hacking as a pretty vile way to behave toward other human beings, and rightly so. But curiously, when nature is the hacker, carrying out part of its relentless program of putting new generations of suffering beings on earth, we get something like breathless celebration.

Makes you wonder how much anyone thinks these things through.

Here is Jesus addressing his eleven remaining disciples in Matthew 28:18-20.

And Jesus came and spake unto them, saying, All power [ἐξουσία] is given unto me in heaven and in earth. Go ye therefore, and teach all nations [ἔθνη], baptizing them in the name of the Father, and of the Son, and of the Holy Ghost: Teaching them to observe all things whatsoever I have commanded [Faustus: ἐνετειλάμην –there’s that word again] you: and, lo, I am with you always, even unto the end of the world. Amen.

So if I get this right, and I see no reason to think I’ve got this wrong, they’re supposed to head out and make everything and everyone Christian. Not explicitly said, but surely implied, is that this process if successful means wiping out all other religions, non-religious worldviews, and ways of life, on a planetwide basis. The great diversity of humankind is to be replaced with a Jesus-based monoculture.

I can think of many names for the aspiration embodied in Jesus’ command, of which “cultural imperialism” is perhaps the most diplomatic.

Here’s a post I thought apropos for Christmas Day, because we all remember whose birthday it is (other than Humphrey Bogart‘s, that is).

Many people think that the core of Christianity can be found in something called The Great Commandment. It’s really two commandments, and can be found in Matthew 22:35-40.

Then one of them, which was a lawyer, asked him a question, tempting him, and saying, Master, which is the great commandment in the law? Jesus said unto him, Thou shalt love the Lord thy God with all thy heart, and with all thy soul, and with all thy mind. This is the first and great commandment. And the second is like unto it, Thou shalt love thy neighbour as thyself. On these two commandments hang all the law and the prophets.

Perhaps “commandment” seems a little strong, but if you look at the underlying Greek you’ll find that the word used by “Matthew” and rendered by King James’s translators as “commandment” is ἐντολή, which is a very commanding word in Greek. Outside of the Christian scriptures it was used by Herodotus (in a verbal form) to describe an order given by the Persian King Cyrus to one of his subordinates.

This meaning raises a question, which no Christian in the past two thousand years has, to my mind anyway, successfully answered, or even raised.

Why on earth would we think of love as something that could be commanded?